Introduksjon til induksjonsbevis

Induksjonsbevis er en viktig metode innen matematikk for å bevise påstander som gjelder for alle naturlige tall. Dette bevisføringsteknikken er grunnleggende i algebra, tallteori og andre grener av matematikk.

Forståelse av induksjonsbevis

Hva er induksjonsbevis?

Induksjonsbevis er en matematisk teknikk som brukes til å bevise at en påstand gjelder for alle naturlige tall.

Hvordan fungerer induksjonsbevis?

Induksjonsbevis består vanligvis av to trinn: basissteget og induksjonstrinnet. Basissteget innebærer å bevise at påstanden er sann for det første naturlige tallet. Deretter antar vi at påstanden er sann for et vilkårlig, men fast naturlig tall k, og bruker dette til å bevise at den også er sann for tallet k + 1.

Enkle induksjonsbevis

Grunnleggende prinsipper

For å utføre et enkelt induksjonsbevis, må vi først vise at påstanden er sann for det første naturlige tallet. Deretter antar vi at den er sann for et vilkårlig, men fast naturlig tall k, og bruker dette til å bevise at den også er sann for tallet k + 1.

Trinn for å utføre et enkelt induksjonsbevis

1. Bevis at påstanden er sann for det første naturlige tallet.
2. Anta at påstanden er sann for et vilkårlig, men fast naturlig tall k.
3. Bruk induksjonshypotesen til å bevise at påstanden er sann for tallet k + 1.

Eksempler på enkle induksjonsbevis

Eksempel 1: Induksjonsbevis for summen av de første n naturlige tallene

La påstanden P(n) være at summen av de første n naturlige tallene er lik n(n+1)/2. Vi kan bevise dette ved induksjon.

Eksempel 2: Induksjonsbevis for den geometriske summen

La påstanden Q(n) være at summen av de første n leddene i en geometrisk rekke er lik (a(1-r^n))/(1-r), hvor a er det første leddet og r er forholdet mellom påfølgende ledd. Dette kan også bevises ved induksjon.

Avanserte induksjonsbevis

Utvidede teknikker

I tillegg til det grunnleggende induksjonsbeviset, er det også avanserte teknikker som sterkt induksjonsbevis og bevis med fallende induksjon.

Bruk av sterke induksjonsbevis

Sterkt induksjonsbevis tillater oss å anta at påstanden er sann for alle tall opp til et bestemt punkt, i stedet for bare ett tall som i vanlig induksjon.

Anvendelser av induksjonsbevis

Innen matematikk

Induksjonsbevis er viktig i matematikk for å bevise en rekke påstander, inkludert egenskaper ved tall og matematiske identiteter.

I datavitenskap og informatikk

Induksjonsbevis spiller også en viktig rolle i datavitenskap og informatikk, spesielt i analysen av algoritmer og kompleksiteten til datastrukturer.

Vanlige feil og hvordan unngå dem

En vanlig feil i induksjonsbevis er å anta at påstanden er sann for et bestemt tall uten tilstrekkelig bevis. For å unngå dette, er det viktig å følge trinnene nøye og være presis i argumentasjonen.

Oppsummering og konklusjon

Induksjonsbevis er en kraftig teknikk innen matematikk og informatikk for å bevise påstander som gjelder for alle naturlige tall. Ved å følge de grunnleggende prinsippene og unngå vanlige feil, kan vi bruke denne metoden til å løse en rekke problemer.

FAQ

1. Hvorfor er induksjonsbevis viktig i matematikk? Induksjonsbevis lar oss bevise påstander som gjelder for alle naturlige tall på en systematisk måte, noe som er avgjørende i mange områder av matematikken.
2. Kan induksjonsbevis brukes til å bevise påstander i andre områder enn matematikk? Ja, induksjonsbevis har også anvendelser i datavitenskap, informatikk og andre vitenskapelige disipliner.
3. Hva er forskjellen mellom vanlig induksjon og sterkt induksjonsbevis? Mens vanlig induksjon antar at en påstand er sann for ett tall og viser at den deretter er sann for det neste, tillater sterkt induksjonsbevis oss å anta at påstanden er sann for flere påfølgende tall samtidig.
4. Kan induksjonsbevis brukes til å bevise alle påstander om naturlige tall? Nei, det er visse typer påstander som ikke kan bevises ved induksjon, for eksempel påstander som gjelder for uendelig mange naturlige tall.
5. Hvordan kan jeg forbedre mine ferdigheter i induksjonsbevis? Å løse flere oppgaver og eksperimenter med ulike typer påstander vil bidra til å styrke dine ferdigheter i induksjonsbevis.

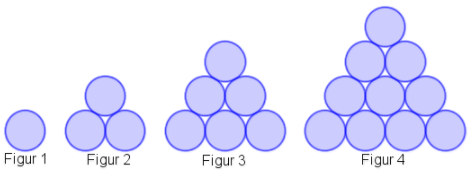
Innledning: En Dyptgående Forståelse av Matematisk Induksjon

Matematisk induksjon er en kraftig teknikk som brukes til å bevise påstander som gjelder for naturlige tall. Denne metoden er essensiell innenfor matematikk, logikk og algoritmeteori. Å forstå og beherske induksjon er avgjørende for å lykkes innen disse disiplinene.

Praktisk Anvendelse av Induksjonsprinsippet

La oss illustrere induksjonsprinsippet med et enkelt eksempel. I et kurs som fokuserer på matematikk, vil induksjonsbevis være en sentral del av pensum. Det er viktig å beherske teknikken for å løse ulike oppgaver knyttet til denne metoden.

Utfyllende Eksempler og Anbefalte Oppgaver

For å få en dypere forståelse av induksjonsbevis, er det nyttig å se på konkrete eksempler og løse oppgaver. Anbefalte oppgaver fra kurs som kalkulus kan gi ytterligere innsikt og trening i bruken av denne metoden.

Veien til Mestring: Praktisk Øvelse og Veiledning

Å bli komfortabel med induksjonsbevis krever tid og praksis. Gjennom å arbeide med ulike oppgaver og få veiledning underveis, kan man utvikle en solid forståelse av denne viktige matematiske teknikken.

Konklusjon

Matematisk induksjon er en fundamental metode innenfor matematikk og relaterte fagområder. Ved å beherske denne teknikken åpner man opp for å løse komplekse problemer og utforske nye matematiske sammenhenger.

Gjennom grundig trening og veiledning kan enhver student utvikle sitt ferdighetsnivå og oppnå mestring i bruken av induksjonsbevis.