Den Ultimative Guiden til Formelen for Fart: En Dybdegående Analyse

I fysikkens fascinerende verden er forståelsen av bevegelse en hjørnestein. Blant de mest grunnleggende og likevel dyptgripende konseptene finner vi fart. Denne tilsynelatende enkle ideen danner grunnlaget for å beskrive hvordan objekter beveger seg i rom og tid. I denne omfattende guiden skal vi dykke dypt inn i formelen for fart, utforske dens definisjon, de ulike enhetene som brukes, praktiske eksempler som illustrerer dens anvendelse i hverdagen, og til og med våge oss inn i mer avanserte konsepter som relaterer seg til fart. Vårt mål er å gi deg en fullstendig og lettfattelig forståelse av dette essensielle fysiske prinsippet.

Hva er Fart? En Grunnleggende Definisjon

Fart defineres som distansen et objekt beveger seg per tidsenhet. Det er et skalært kvantum, noe som betyr at det kun har en størrelse og ingen retning. Dette skiller det fra hastighet, som er et vektorkvantum og dermed spesifiserer både størrelse og retning på bevegelsen. Når vi snakker om hvor raskt noe beveger seg uten å spesifisere retningen, refererer vi til farten. For eksempel, hvis en bil kjører med 60 kilometer i timen, beskriver dette bilens fart. Hvis vi sier at bilen kjører 60 kilometer i timen nordover, beskriver vi bilens hastighet.

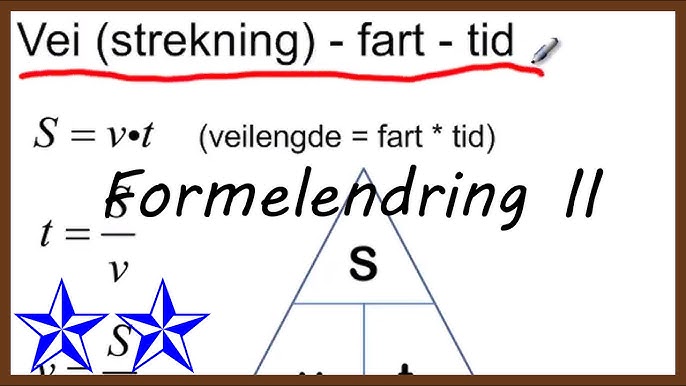
Den Matematiske Representasjonen: Formelen for Fart

Den grunnleggende formelen for fart er bemerkelsesverdig enkel og uttrykkes som:

$$ \text{Fart} = \frac{\text{Distanse}}{\text{Tid}} $$

Hvor:

• Fart (vanligvis representert med symbolet $v$ eller $s$) er målet på hvor raskt et objekt beveger seg.
• Distanse (vanligvis representert med symbolet $d$ eller $s$) er den totale lengden objektet har beveget seg.
• Tid (vanligvis representert med symbolet $t$) er tidsintervallet som bevegelsen har funnet sted over.

Denne formelen er fundamental i fysikk og brukes i et bredt spekter av applikasjoner, fra enkle beregninger av en bils fart til mer komplekse analyser av partikkelbevegelser.

Enheter for Fart: Et Internasjonalt Perspektiv

For å sikre konsistens og klarhet i vitenskapelige og tekniske sammenhenger er det viktig å bruke standardiserte enheter for fart. Det internasjonale enhetssystemet (SI-systemet) definerer meter per sekund (m/s) som standardenheten for fart. Imidlertid brukes også andre enheter i ulike sammenhenger, avhengig av praktiske hensyn og tradisjon.

Vanlige Enheter for Fart og Deres Konverteringer

• Meter per sekund (m/s): Dette er SI-enheten. Den representerer distansen i meter som et objekt beveger seg på ett sekund.

• Kilometer per time (km/t): Denne enheten er vanlig for å beskrive farten til kjøretøy og i mange hverdagsituasjoner. Konverteringen til m/s er: 1 km/t = $\frac{1000 \text{ m}}{3600 \text{ s}} = \frac{1}{3.6} \text{ m/s} \approx 0.2778 \text{ m/s}$.
• Miles per hour (mph): Denne enheten brukes i mange engelskspråklige land, spesielt for veitrafikk. Konverteringen til km/t er: 1 mph $\approx$ 1.609 km/t. Konverteringen til m/s er: 1 mph $\approx$ 0.447 m/s.
• Knop (kn): Denne enheten brukes primært innen maritim og luftfart. En knop er definert som én nautisk mil per time. En nautisk mil er omtrent 1.852 kilometer. Dermed er 1 knop $\approx$ 1.852 km/t $\approx$ 0.514 m/s.

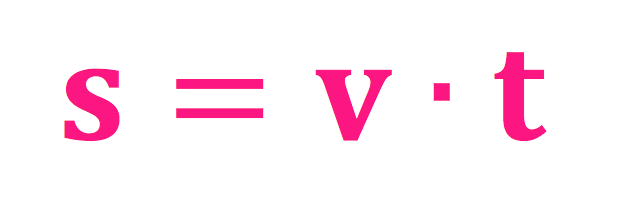
Forståelsen av disse enhetene og hvordan man konverterer mellom dem er avgjørende for å løse problemer som involverer fart og for å tolke informasjon som presenteres i ulike enheter.

Gjennomsnittsfart vs. Momentanfart: Nyanser i Bevegelse

Når vi diskuterer fart, er det viktig å skille mellom gjennomsnittsfart og momentanfart. Disse to konseptene gir oss forskjellig informasjon om et objekts bevegelse.

Gjennomsnittsfart: Et Helhetsbilde av Bevegelsen

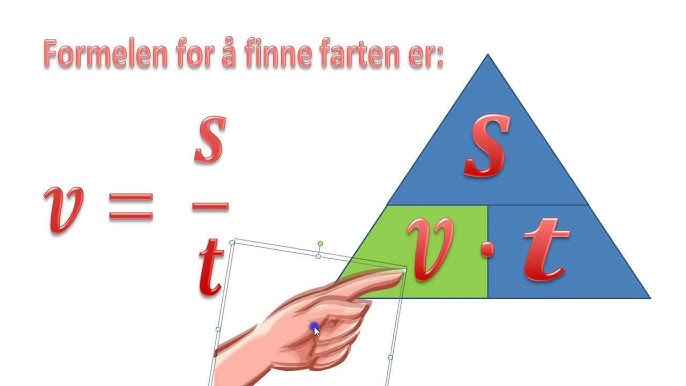
Gjennomsnittsfart beregnes over et gitt tidsintervall og tar hensyn til den totale distansen som er tilbakelagt og den totale tiden som har gått. Formelen for gjennomsnittsfart er den samme som den grunnleggende formelen for fart:

$$ \text{Gjennomsnittsfart} = \frac{\text{Total distanse}}{\text{Total tid}} $$

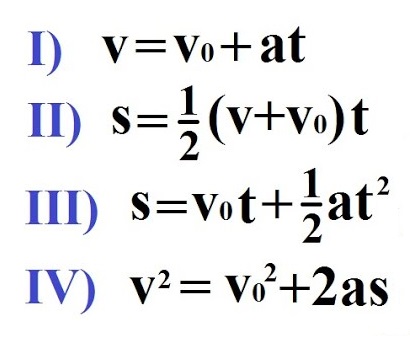
Gjennomsnittsfarten gir oss et overordnet bilde av hvor raskt et objekt har beveget seg i løpet av en viss periode, men den sier ingenting om variasjoner i farten underveis.

Eksempel på Gjennomsnittsfart

Tenk deg at du kjører bil fra by A til by B, en distanse på 100 kilometer. Turen tar deg 2 timer. Da er gjennomsnittsfarten din:

$$ \text{Gjennomsnittsfart} = \frac{100 \text{ km}}{2 \text{ timer}} = 50 \text{ km/t} $$

Dette betyr ikke at du har kjørt nøyaktig 50 km/t hele tiden. Du kan ha kjørt saktere i noen områder (f.eks. i tettbygd strøk) og raskere i andre (f.eks. på motorveien). Gjennomsnittsfarten gir bare et gjennomsnitt over hele turen.

Momentanfart: Farten i et Øyeblikk

Momentanfart er farten til et objekt på et spesifikt tidspunkt. Den beskriver hvor raskt objektet beveger seg akkurat i det øyeblikket vi observerer det. For å forstå momentanfart intuitivt, tenk på speedometeret i en bil. Speedometeret viser bilens fart i det øyeblikket du ser på det – dette er momentanfarten.

Matematisk Tilnærming til Momentanfart

Matematisk sett kan momentanfart defineres som grensen av gjennomsnittsfarten når tidsintervallet nærmer seg null. Hvis vi har en funksjon $d(t)$ som beskriver posisjonen til et objekt som en funksjon av tid, er momentanfarten $v(t)$ gitt ved den deriverte av posisjonen med hensyn til tid:

$$ v(t) = \lim_{\Delta t \to 0} \frac{\Delta d}{\Delta t} = \frac{dd}{dt} $$

Dette konseptet er sentralt i differensialregning og gir oss et kraftfullt verktøy for å analysere bevegelse med varierende fart.

Praktiske Eksempler på Bruk av Formelen for Fart

Formelen for fart er ikke bare en abstrakt matematisk konstruksjon; den har utallige praktiske anvendelser i hverdagen og i ulike vitenskapelige og tekniske disipliner.

Eksempel 1: Beregning av Reisetid

La oss si at du planlegger en biltur på 300 kilometer og du forventer å kjøre med en gjennomsnittsfart på 80 km/t. For å finne ut hvor lang tid turen vil ta, kan du omorganisere formelen for fart:

$$ \text{Tid} = \frac{\text{Distanse}}{\text{Fart}} $$

Setter vi inn verdiene får vi:

$$ \text{Tid} = \frac{300 \text{ km}}{80 \text{ km/t}} = 3.75 \text{ timer} $$

Dermed vil turen ta deg 3 timer og 45 minutter (0.75 timer $\times$ 60 minutter/time = 45 minutter).

Eksempel 2: Bestemmelse av Fart fra Distanse og Tid

En løper fullfører en 10 kilometer lang løype på 45 minutter. For å finne gjennomsnittsfarten til løperen i meter per sekund, må vi først konvertere enhetene:

• Distanse: 10 km = 10 $\times$ 1000 m = 10000 m
• Tid: 45 minutter = 45 $\times$ 60 sekunder = 2700 s

Nå kan vi bruke formelen for fart:

$$ \text{Fart} = \frac{10000 \text{ m}}{2700 \text{ s}} \approx 3.70 \text{ m/s} $$

Løperens gjennomsnittsfart var omtrent 3.70 meter per sekund.

Eksempel 3: Navigasjon og Fart i Luftfart

Et fly flyr en distanse på 500 nautiske mil på 1.5 timer. For å finne flyets gjennomsnittsfart i knop:

$$ \text{Fart} = \frac{500 \text{ nautiske mil}}{1.5 \text{ timer}} \approx 333.33 \text{ knop} $$

Dette eksemplet illustrerer hvordan fart er en kritisk parameter innen navigasjon og transport.

Relativ Fart: Bevegelse i Perspektiv

Konseptet relativ fart oppstår når vi observerer bevegelsen til et objekt fra et referansesystem som selv er i bevegelse. Den relative farten mellom to objekter er farten til det ene objektet sett fra det andre. Dette konseptet er viktig i mange situasjoner, for eksempel i trafikk, navigasjon og i studiet av himmellegemer.

Beregning av Relativ Fart

Hvis to objekter beveger seg langs den samme linjen, kan den relative farten beregnes ved å subtrahere farten til det ene objektet fra farten til det andre. La $v_A$ være farten til objekt A og $v_B$ være farten til objekt B. Da er den relative farten til A sett fra B ($v_{A/B}$) gitt ved:

$$ v_{A/B} = v_A – v_B $$

Retningen er viktig her. Hvis objektene beveger seg i samme retning, vil den relative farten være mindre enn de individuelle fartene. Hvis de beveger seg i motsatt retning, vil den relative farten være større enn de individuelle fartene.

Eksempel på Relativ Fart

To biler kjører på en motorvei i samme retning. Bil A kjører med 90 km/t og bil B kjører med 70 km/t. Den relative farten til bil A sett fra bil B er:

$$ v_{A/B} = 90 \text{ km/t} – 70 \text{ km/t} = 20 \text{ km/t} $$

Dette betyr at for passasjerene i bil B ser det ut som om bil A nærmer seg med en fart på 20 km/t.

Hvis bil A kjører med 90 km/t nordover og bil B kjører med 70 km/t sørover, er den relative farten til bil A sett fra bil B:

$$ v_{A/B} = 90 \text{ km/t} – (-70 \text{ km/t}) = 90 \text{ km/t} + 70 \text{ km/t} = 160 \text{ km/t} $$

I dette tilfellet ser det ut som om bil A nærmer seg bil B med en mye høyere fart.

Forholdet Mellom Fart og Hastighet: En Viktig Distinksjon

Selv om begrepene fart og hastighet ofte brukes om hverandre i dagligtalen, har de distinkte betydninger i fysikk. Som nevnt tidligere, er fart et skalært kvantum som kun beskriver hvor raskt et objekt beveger seg. Hastighet, derimot, er et vektorkvantum som spesifiserer både farten og retningen til bevegelsen.

Vektorrepresentasjon av Hastighet

Hastighet kan representeres som en vektor, der lengden på vektoren tilsvarer farten (størrelsen), og pilens retning angir bevegelsesretningen. For eksempel, en hastighet på 20 m/s østover er forskjellig fra en hastighet på 20 m/s nordover, selv om farten er den samme i begge tilfeller.

Endring i Hastighet: Akselerasjon

Endring i hastighet over tid kalles akselerasjon. Siden hastighet er en vektor, kan akselerasjon oppstå enten ved en endring i farten, en endring i retningen, eller begge deler. Et objekt som kjører i en sirkel med konstant fart akselererer kontinuerlig fordi retningen på hastigheten endres hele tiden.

Formelen for gjennomsnittlig akselerasjon er:

$$ \text{Gjennomsnittlig akselerasjon} = \frac{\text{Endring i hastighet}}{\text{Tidsintervall}} = \frac{\Delta \mathbf{v}}{\Delta t} $$

Hvor $\Delta \mathbf{v}$ er endringen i hastighetsvektoren og $\Delta t$ er tidsintervallet.

Konstant Fart vs. Variabel Fart: Bevegelsens Natur

Bevegelsen til et objekt kan enten være med konstant fart eller variabel fart. Disse to typene bevegelse krever forskjellige tilnærminger for analyse og beskrivelse.

Konstant Fart: Enkel og Forutsigbar Bevegelse

Når et objekt beveger seg med konstant fart, betyr det at farten forblir den samme over tid. I dette tilfellet er gjennomsnittsfarten lik momentanfarten til enhver tid. Bevegelse med konstant fart skjer i en rett linje med uendret hastighetsvektor (ingen akselerasjon).

Eksempler på Bevegelse med Konstant Fart (Idealisert)

• Et romskip som beveger seg i det ytre rom uten påvirkning fra eksterne krefter (i henhold til Newtons første lov).
• En gjenstand som glir