Den Ultimate Guiden til Induksjonsbevis: Oppgaver, Strategier og Dybdeforståelse

Velkommen til vår omfattende ressurs om induksjonsbevis. Denne guiden er designet for å gi deg en dyp og grundig forståelse av prinsippene bak matematiske induksjonsbevis, samt et vell av oppgaver med detaljerte løsninger. Enten du er en student som strever med dette fundamentale konseptet, en lærer som søker etter undervisningsmateriell, eller rett og slett en matematikkentusiast som ønsker å utvide dine kunnskaper, vil denne artikkelen gi deg verktøyene og innsiktene du trenger for å mestre induksjonsbevis til fulle.
Hva er Induksjonsbevis? En Grunnleggende Innføring
Induksjonsbevis er en kraftfull teknikk innen matematikken som brukes for å bevise at en påstand gjelder for alle naturlige tall (eller en delmengde av dem, som for eksempel alle heltall større enn eller lik et visst tall). Metoden baserer seg på et prinsipp som kan sammenlignes med dominoeffekten: hvis du kan vise at den første dominoen faller (grunntrinnet), og at fallet til en hvilken som helst domino fører til at den neste også faller (induksjonsskrittet), da må alle dominoene falle.

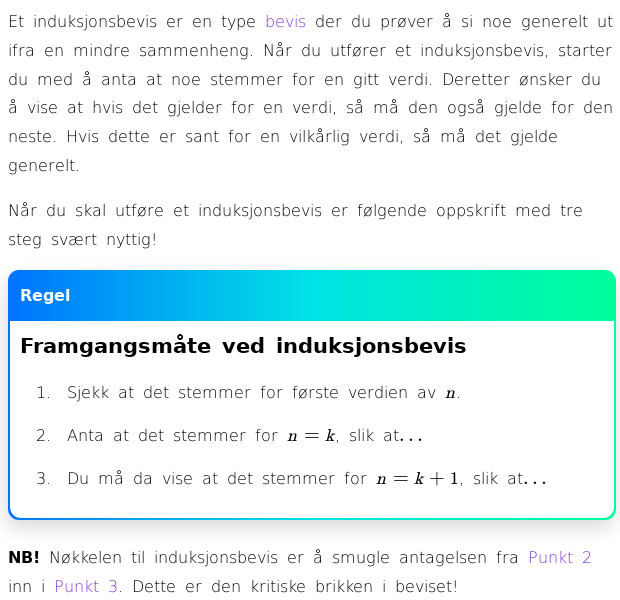
Mer formelt består et induksjonsbevis typisk av tre hovedtrinn:
- Grunntrinnet (Basistrinnet): Her viser vi at påstanden er sann for det første naturlige tallet (vanligvis n \= 1, men det kan også være n \= 0 eller et annet startpunkt).
- Induksjonshypotesen: Vi antar at påstanden er sann for et vilkårlig naturlig tall k. Denne antagelsen kalles induksjonshypotesen.
- Induksjonsskrittet: Ved å bruke induksjonshypotesen viser vi at påstanden også må være sann for det neste naturlige tallet, k \+ 1.
Når disse tre trinnene er fullført, har vi ved det matematiske induksjonsprinsippet bevist at påstanden er sann for alle naturlige tall fra og med startpunktet i grunntrinnet.

Grunntrinnet i Detalj: Etablering av Basisen
Grunntrinnet er fundamentet for ethvert induksjonsbevis. Det handler om å verifisere at påstanden vi ønsker å bevise faktisk holder for den første verdien av n i det aktuelle settet av naturlige tall. Dette er ofte det enkleste trinnet, men det er likevel essensielt å utføre det korrekt. Hvis grunntrinnet ikke holder, faller hele beviset sammen.
Valget av startverdi for n avhenger av påstanden som skal bevises. Hvis påstanden gjelder for alle naturlige tall, starter vi med n \= 1. Hvis påstanden gjelder for alle ikke-negative heltall, starter vi med n \= 0. Det finnes også tilfeller hvor påstanden først gjelder fra et visst tall n\_0 \> 1, og da vil grunntrinnet være å vise at påstanden er sann for n \= n\_0.
For å gjennomføre grunntrinnet, substituerer vi ganske enkelt startverdien for n inn i påstanden og sjekker om likheten holder, eller om ulikheten er sann, avhengig av hva påstanden hevder.
Eksempel på Grunntrinn
La oss bevise ved induksjon at summen av de n første positive heltallene er gitt ved formelen \\frac\{n\(n\+1\)\}\{2\}.
Påstand: 1 \+ 2 \+ \\dots \+ n \= \\frac\{n\(n\+1\)\}\{2\} for alle n \\ge 1.
Grunntrinn (n \= 1):
Venstre side (VS) er bare det første tallet, som er 1.
Høyre side (HS) er \\frac\{1\(1\+1\)\}\{2\} \= \\frac\{1 \\cdot 2\}\{2\} \= 1.
Siden VS = HS (1 = 1), er påstanden sann for n \= 1. Dermed har vi fullført grunntrinnet.
Induksjonshypotesen: Antagelsens Kraft
Induksjonshypotesen er et avgjørende steg i induksjonsbeviset. Her antar vi at påstanden vi ønsker å bevise er sann for et vilkårlig, men spesifikt naturlig tall k, hvor k er større enn eller lik startverdien i grunntrinnet. Det er viktig å understreke at vi ikke beviser at påstanden er sann for k i dette trinnet; vi bare *antager* det. Denne antagelsen er vårt utgangspunkt for det neste trinnet, induksjonsskrittet.

Kraften i induksjonshypotesen ligger i at den gir oss et verktøy — en etablert sannhet (i hvert fall for k) — som vi kan bruke til å vise at påstanden også må holde for det neste naturlige tallet, k \+ 1. Uten denne antagelsen ville det være vanskelig, om ikke umulig, å bygge broen fra et generelt tilfelle til det neste.
Når vi formulerer induksjonshypotesen, skriver vi ganske enkelt ned påstanden vi ønsker å bevise, men erstatter n med k. For eksempel, hvis påstanden er P\(n\), så er induksjonshypotesen P\(k\).
Eksempel på Induksjonshypotese
Fortsetter vi med eksempelet om summen av de n første positive heltallene:
Påstand: 1 \+ 2 \+ \\dots \+ n \= \\frac\{n\(n\+1\)\}\{2\}.
Induksjonshypotese: Anta at påstanden er sann for et vilkårlig naturlig tall k \\ge 1. Det vil si, vi antar at:
1 \+ 2 \+ \\dots \+ k \= \\frac\{k\(k\+1\)\}\{2\}
Denne antagelsen skal vi nå bruke i neste trinn for å vise at påstanden også holder for k \+ 1.
Induksjonsskrittet: Broen til Neste Tall
Induksjonsskrittet er selve kjernen i induksjonsbeviset. Her bruker vi induksjonshypotesen (antagelsen om at påstanden er sann for n \= k) for å bevise at påstanden også må være sann for det neste naturlige tallet, n \= k \+ 1. Målet er å manipulere uttrykket for n \= k \+ 1 slik at vi kan inkorporere induksjonshypotesen på en eller annen måte og deretter vise at det resulterende uttrykket stemmer overens med påstanden for n \= k \+ 1.
Strategien i induksjonsskrittet varierer avhengig av påstanden som skal bevises. For summeformler handler det ofte om å legge til det \(k\+1\)-te leddet på begge sider av induksjonshypotesen og deretter manipulere algebraisk for å komme frem til den ønskede formelen for n \= k \+ 1. For påstander om delbarhet kan det innebære å faktorisere uttrykk eller bruke egenskaper ved divisjon. For ulikheter må vi kanskje bruke induksjonshypotesen for å erstatte deler av uttrykket og deretter bruke ytterligere ulikheter for å nå konklusjonen.
Det er viktig å være nøye med de algebraiske manipulasjonene og logikken i dette trinnet. Hvert steg må være velbegrunnet og føre oss nærmere målet om å vise at påstanden holder for n \= k \+ 1.
Eksempel på Induksjonsskritt
Fortsetter vi med eksempelet om summen av de n første positive heltallene:
Induksjonshypotese: Anta at 1 \+ 2 \+ \\dots \+ k \= \\frac\{k\(k\+1\)\}\{2\} for et vilkårlig k \\ge 1.
Induksjonsskritt: Vi ønsker å vise at påstanden også er sann for n \= k \+ 1, det vil si at:
1 \+ 2 \+ \\dots \+ \(k \+ 1\) \= \\frac\{\(k \+ 1\)\(\(k \+ 1\) \+ 1\)\}\{2\} \= \\frac\{\(k \+ 1\)\(k \+ 2\)\}\{2\}
Vi starter med venstre side av denne likheten og bruker induksjonshypotesen:
1 \+ 2 \+ \\dots \+ \(k \+ 1\) \= \(1 \+ 2 \+ \\dots \+ k\) \+ \(k \+ 1\)
Nå kan vi erstatte summen 1 \+ 2 \+ \\dots \+ k med \\frac\{k\(k\+1\)\}\{2\} fra induksjonshypotesen:
\= \\frac\{k\(k\+1\)\}\{2\} \+ \(k \+ 1\)
For å kombinere disse to leddene, finner vi en felles nevner:
\= \\frac\{k\(k\+1\)\}\{2\} \+ \\frac\{2\(k \+ 1\)\}\{2\}
\= \\frac\{k\(k\+1\) \+ 2\(k \+ 1\)\}\{2\}
Nå kan vi faktorisere ut \(k \+ 1\) fra telleren:
\= \\frac\{\(k \+ 1\)\(k \+ 2\)\}\{2\}
Dette er nøyaktig høyre side av påstanden for n \= k \+ 1. Dermed har vi vist at hvis påstanden er sann for k, så er den også sann for k \+ 1.
Konklusjonen: Sammenfatning av Beviset
Når vi har fullført både grunntrinnet og induksjonsskrittet, kan vi trekke konklusjonen basert på det matematiske induksjonsprinsippet. Konklusjonen skal tydelig angi at siden vi har vist at påstanden er sann for startverdien (grunntrinnet), og at hvis den er sann for et vilkårlig naturlig tall k, så er den også sann for det neste naturlige tallet k \+ 1 (induksjonsskrittet), da må påstanden være sann for alle naturlige tall fra og med startverdien.
I vårt eksempel med summen av de n første positive heltallene, ville konklusjonen være:
Konklusjon: Siden vi har vist at påstanden er sann for n \= 1 (grunntrinnet), og at hvis den er sann for et vilkårlig naturlig tall k \\ge 1, så er den også sann for n \= k \+ 1 (induksjonsskrittet), følger det fra det matematiske induksjonsprinsippet at formelen 1 \+ 2 \+ \\dots \+ n \= \\frac\{n\(n\+1\)\}\{2\} er sann for alle naturlige tall n \\ge 1.
En klar og tydelig konklusjon er viktig for å fullføre beviset på en formell og korrekt måte.
Varianter av Induksjonsbevis: Utvidet Anvendelse
Selv om det grunnleggende prinsippet for induksjonsbevis er det samme, finnes det flere varianter som er nyttige for å håndtere ulike typer påstander:
Sterk Induksjon (Full Induksjon)
Ved sterk induksjon antar vi i induksjonshypotesen at påstanden er sann for *alle* naturlige tall opp til og med k, ikke bare for k alene. Deretter bruker vi denne sterkere antagelsen til å vise at påstanden er sann for k \+ 1. Sterk induksjon er spesielt nyttig når sannheten til påstanden for k \+ 1 avhenger av sannheten til påstanden for flere tidligere verdier enn bare k.
Induksjon med Andre Startpunkter
Som nevnt tidligere, trenger ikke induksjonsbevis alltid å starte ved n \= 1. Hvis en påstand gjelder for alle heltall større enn eller lik et visst tall n\_0, vil grunntrinnet være å vise at påstanden er sann for n \= n\_0, og induksjonsskrittet vil vise at hvis den er sann for k \\ge n\_0, så er den også sann for k \+ 1.
Baklengs Induksjon
Baklengs induksjon brukes for å bevise at en påstand gjelder for alle naturlige tall ved å først vise at den gjelder for et uendelig antall tall (ofte ved å bevise den for alle potenser av 2) og deretter vise at hvis den gjelder for k \+ 1, så gjelder den også for k.
Dobbel Induksjon
Dobbel induksjon brukes for påstander som avhenger av to naturlige tall, for eksempel P\(m, n\). Beviset innebærer vanligvis å utføre induksjon over en av variablene mens den andre holdes konstant, og deretter utføre induksjon over den andre variabelen.
Strategier for Å Løse Oppgaver med Induksjonsbevis

Å mestre induksjonsbevis